The "Explore MTBoS" challenge is to blog a lesson. I chose to report on today's lesson. It's a skill lesson - adding/subtracting rational expressions. We've analyzed graphs, discussed asymptotes and holes, and we are going to work on application problems in a few days... work, travel, cost, mixture, and inverse variation.
But in the middle of graph analysis and problem solving ... we have to learn the skill of adding/subtracting/multiplying/dividing expressions and solving equations. We'll only spend 2 class periods on these basic skills.
This is one of those less glamorous lessons.
Today I have leftover popcorn from a fundraiser at Saturday's academic competitions. I invite students to scoop out a cup and munch while we work. I tell them I hope that every time they smell/taste popcorn in the near future they remember how to find the LCD of a rational expression.
My students are 9th and 10th graders - not too far removed from the middle school - so I ask them about their feelings towards fractions, and how they learned to add fractions.
I give them the problem, 1/6 + 4/15, and ask them to tell their neighbor how they found the sum.
I factor the denominators ... and then I launch into a story about my neighbor. The story is borrowed directly from George Woodbury. By the third class, I guess I get good at it ... they are hanging on every word ... and clap when I make the connection to the fractions on the board. Later I hear them talking about the upgraded model of the grill (x + 4) vs (x + 4) squared as they are finding sums.
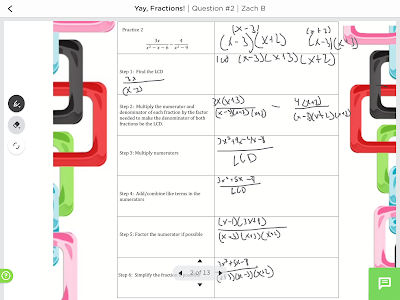
Then we jump into ClassKick, my favorite iPad app. I've prepared slides for taking notes. On those slides I demonstrate step by step how to add/subtract rational expressions. The students follow along, working the problems with me.

Then I provide 2 slides with problems worked out with errors. I ask students to find the errors, and then check in with their neighbors to see if they agree. If they don't agree I encourage them to talk it out.

In these error problems we discuss the excluded values. We've already studied asymptotes and holes so students are familiar with the concept of excluded values. I ask students, "Why are values are excluded from the addends?" I ask again - would those values be excluded even if the simplified sum was not affected by the values?

Next we stop for a couple of minutes of reflection. What is the muddiest point for you? Or on what step are you have the most difficulty? And on a scale of 1 - 10, what is your confidence level at this time?
It's at this point that students' actions diverge depending on their confidence levels. On the next slide I give them 3 videos I found online that explain adding/subtracting rationals. None of the videos are long ... just one problem each. I tell students that if their confidence level is less than a five, I want them to watch at least one video, and all three if they prefer. Then move on into the class practice. For others who rated themselves high on confidence they begin working on the class examples. Differentiation is based on students' perception of their understanding.

As students work on the class examples, I give simple "sticker" feedback electronically or help them at their desks as requested. Students who chose to watch a video get started on the problems a few minutes later. Some students finish early and are asked to either help others or work on their BrainGenie goal which reinforces the skill. I monitor student progress visually from the ClassKick projection showing everyone's work, and also specifically as I tour the room.
Overall the lesson went well. Students will need more practice ... and that's difficult with our schedule. I'm hoping they choose to do the 10 problems I assigned for homework. I won't grade them ... I gave them worked out solutions. They know they'll complete a learning check in the next class on this skill.
I wish I had had one more reflective time at the end ... has your confidence level improved with this practice today?
Exciting times in Algebra 2.


Classkick seems pretty cool. Is is only iPad? Do you need to be 1-1?
ReplyDeleteIt is only iPad. You could use this app in a partner situation.
DeleteThank you for sharing the story from George Woodbury. I love it, and I agree that it is memorable (and something kids can relate too -- I see my own trying to keep up with each other!).
ReplyDeleteDo you have similar stories you tell for other types of lessons? Or just a few handpicked goodies?
More often than not, my stories are impromptu. I don't have specific strategy stories ... although collecting those would be a worthy project!
DeleteThis comment has been removed by a blog administrator.
ReplyDelete